TRASPLANTE DE MÉDULA ÓSEA

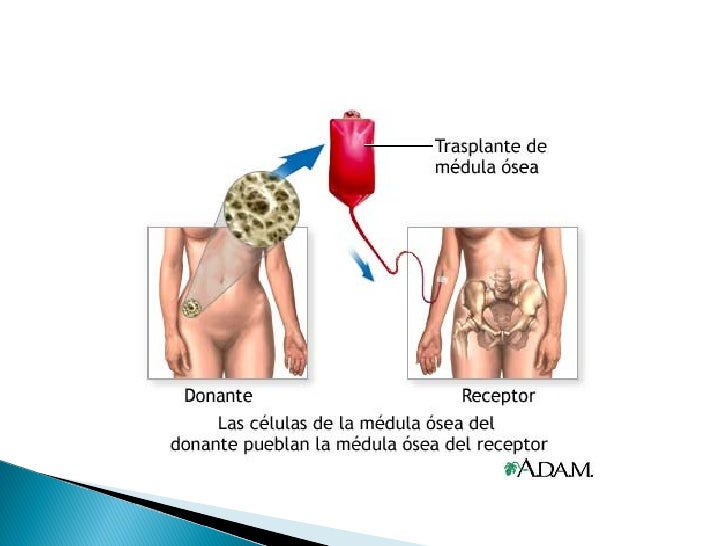
Un trasplante es un procedimiento para reemplazar la médula ósea dañada o destruida por células madre de médula ósea sana.

La médula ósea es el tejido graso y blando que se encuentra dentro de los huesos. La médula ósea produce glóbulos rojos y las células madre son células inmaduras en la médula ósea que dan origen a todas las células sanguíneas diferentes. 

El trasplante es un tratamiento médico en el que no hay cirugía. Es necesario administrar una dosis de quimioterapia mucho más alta de la que cualquier ser humano puede tolerar, por ello, las células progenitoras solo se obtienen de médula ósea en casos muy especiales.

Posibles tratamientos con células madre

El único tratamiento aprobado hasta el momento con empleo de células madre, en cualquier parte del mundo, es el del trasplante alogénico de Células Progenitoras Hematopoyéticas (CPH) de un donante a un paciente, ya sean las mismas tomadas de la médula ósea, de la sangre periférica o de la sangre del cordón umbilical. Estos trasplantes son un recurso terapéutico aceptado, utilizado y con buenos resultados.

Por otra parte no existe ninguna evidencia clínica que indique su eficacia terapéutica en otras enfermedades como Parkinson, Alzheimer, diabetes, etcétera. Todo uso de células madre que no sea el trasplante de médula ósea, es experimental.

• Tipos de trasplante según el donante: 
• Trasplante singénico. Es el realizado entre hermanos gemelos univitelinos. No hay posibilidad de rechazo ya que estos hermanos son genéticamente idénticos. es un tipo de trasplante poco común ya que es poco frecuente que el paciente tenga un hermano gemelo univitelino.
• Trasplante alogénico. Es el que se da entre dos individuos con diferencias genéticas pero con el mayor parecido posible. Es decir, hermanos, otros familiares, donantes haploidénticos, donantes no emparentados obtenidos de los registros nacionales de médula.
• Autotrasplante: Consiste en la extracción de células progenitoras del propio paciente antes de la administración del tratamiento. Tras el tratamiento serán reinfundidas dichas células.

INDICACIONES PARA EL TRASPLANTE CON CÉLULAS MADRE

El trasplante de CPH es un tratamiento establecido en una serie de enfermedades hematológicas en las que se utiliza de forma habitual, ya sea como tratamiento convencional o alternativo. 

Existen una serie de enfermedades para las cuales su aplicación es necesaria, dichas enfermedades son las siguientes: 

Neoplasias	Otras enfermedades
LLA (Leucemia linfoide aguda)	Enfermedades autoinmunes
LMC (Leucemia mieloide crónica)	Anemia aplásica
SMD (Síndromes mielodisplásicos)	Hemoglobinuria Paroxística Nocturna
SMP (Síndromes mieloproliferativos)	Anemia de Fanconi
Linfoma	Anemia de Blackfan.Diamond
Tumores sólidos	Talasemia
LLC (Leucemia linfática crónica)	Inmunodeficiencias
LMMJ (Leucemia mielomonocítica juvenil)	Síndrome de Wiskott-Alddrich
Mieloma	Errores congénitos del metabolismo

BIBLIOGRAFÍA

1. Medline Plus [Internet] Todd Gersten, MD, Hematology/Oncology, Florida Cancer Specialists & Research Institute, Wellington, FL. [Actualizado: 03/10/17; citado:07/11/17]Disponible en: https://medlineplus.gov/spanish/ency/article/003009.htm
2. Instituto Nacional Central Único Coordinador de Ablación e Implante. [Internet]. Información sobre tratamientos con células madre. Ministerio de Salud; República Argentina. [Citado: 12/11/17] Disponible en: http://www.incucai.gov.ar/files/docs-incucai/Celulas-madre/05-doc_celulas_madre.pdf

¿QÚE ES UN DRENAJE QUIRÚRGICO Y QUÉ TIPOS EXISTEN?

Un drenaje quirúrgico es un método o procedimiento operatorio artificial que se lleva a cabo para evitar que se cierre una herida con foco infeccioso, o favorecer la expulsión de materia líquida, semilíquida o gaseosa de una cavidad corporal o tejido al exterior (dificultando su posterior acúmulo), las cuales retardarían o impedirían la normal cicatrización, y que conllevarían a un empeoramiento de la persona por ser nocivas. De esta manera, lo que se intenta evitar son los riesgos de infecciones, fenómenos compresivos o estasis local.

Su acción más simple es aquella donde se deja que el tejido o la cavidad drene directamente hacia el exterior, o hacia el interior mediante comunicación libre directa hasta que termina el flujo de material drenado.

En otros casos es necesario utilizar un drenaje artificial, donde el líquido fluye por el material introducido en el lecho quirúrgico.

Los drenajes pueden tener dos funciones principales: profiláctica y terapéutica.

Drenaje profiláctico: Sirve principalmente para la prevención contra los posibles acúmulos de diversas toxinas y secreciones de todo tipo que pueden darse tras una operación.

Drenaje terapéutico: Tiene el mismo fin que el drenaje profiláctico, pero se usa momentos antes de la intervención.

Existen varios tipos de drenajes:

• Drenaje abierto; también llamado simple, pasivo o sin aspiración. Normalmente se usa para drenar pequeñas cantidades de materia, que estén muy localizadas. Presenta algunos inconvenientes, como favorecer la infección de fuera a dentro; por otro lado, ya que no se trata de un procedimiento medible, no se puede saber cuál es la cantidad de fluido drenado. Dentro de este tipo de drenaje, existen a su vez, varios subtipos: 
• Drenaje de Penrose: Se usa un tubo de látex (disponible en varios diámetros), que va junto a un apósito donde se vierten los líquidos drenados. Funciona mediante el principio de la capilaridad, éste se aloja en la zona de mayor declive, y a partir de aquí, los líquidos atraviesan de forma pasiva la superficie. Este método no perjudica a los tejidos cercanos y provoca poca irritación tisular. Se usa para evacuar sangre o pus, pero su mayor utilidad es en el drenaje de abscesos de partes blandas.
• Drenaje en láminas: se introducen las láminas de látex, y el líquido asciende por gravedad hasta quedar recogido en gasas o compresas.
• Drenaje capilar: Mediante tiras de gasas cubiertas con una compresa, donde se ejerce la fuerza de la capilaridad, y el líquido drenado se absorbe. Con esta técnica se intenta evitar la infección de “fuera a dentro”. En este caso, se debe evitar cubrir la cavidad totalmente con gasas ya que se podría obstruir. Como la gasa se empapa rápidamente, hay que cambiarlas continuamente.
• Tubos de drenaje: Son tubos de silicona, caucho o polietileno de entre 3 y 15 mm de diámetro. Estos se conectan a un sistema de aspiración, y el líquido se mueve por fuerza de la gravedad. Dentro de éste, encontramos el conocido como el drenaje de Kehr.
• El drenaje de Kehr es un drenaje pasivo que actúa para descompresión del colédoco tras la cirugía de vías biliares cuando existe posible retracción posoperatoria del orificio seccionado en el colédoco. Consiste en un tubo blando en forma de T de distintos calibres según las necesidades. Los extremos más cortos canalizan las vías biliares, y el más largo sale afuera atravesando la pared abdominal.
• Drenajes cerrados, activos, de succión, con aspiración de baja presión o bajo vacío. Suelen ser drenajes rígidos de silicona o polvinilo conectados a un sistema de succión activo. En el exterior se encuentra el sistema de vacío a presión negativa que al conectarse, se da una succión continua a baja presión, por donde fluye el líquido, y lo que permite también la cuantificación y el estudio del drenado. 
• Drenaje tipo Redón: Se utiliza un tubo rígido multiperforado conectado al sistema de vacío. 
• Drenaje tipo Jackson-Pratt: Un catéter de silicona flexible, blanco y multiperforado. 
• Drenajes aspirativos, dependen del lugar de actuación
• Drenaje abdominal; consta de varios tubos de grueso calibre y varias luces para poder irrigar y aspirar durante el procedimiento. Se componen de un tubo exterior multiperforado en su extremo distal, una zona intermedia y otro tubo interior que facilita la aspiración junto a la toma de aire.
• Drenaje torácico; consiste en un tubo de plástico rígido pero flexible, multiperforado y de diámetro variable. Dichos tubos se conectan a un sistema recolector formado por tres cámaras conectadas entre sí mediante válvulas unidireccionales del paciente al sistema de succión. Este sistema permite la salida del aire y líquido del tórax evitando su reingreso.
• Drenajes percutánteos, se basan en la localización radiológica de la zona a drenar. A continuación, tras la anestesia local, se punciona con una aguja fina la pared y se desliza una guía metálica hasta localizar la zona a drenar. Posteriormente se introduce el catéter a través de la guía que posteriormente se retira. Por último, se extraen el material de drenaje junto con la localización radiológica.

BIBLIOGRAFÍA

1. Manuel Durán, Emilia Cancer, Enrique Moro, Julia Álvarez. Material quirúrgico auxiliar. Jaime Arias Pérez. Propedéutica quirúrgica. Preoperatorio, operatorio, postoperatorio. Madrid: Tébar; 2004. P. 163-194.]
2. [J. Díaz Aguado. Drenajes quirúrgicos. Manual básico de enfermería: técnica y quirúrgica. Madrid: Díaz de Santos; 1998. Capítulo 13; Pág. 69-76]

HIGIENE BUCODENTAL INFANTIL

Una buena higiene bucal debería empezar a una edad más temprana de lo que habitualmente se suele pensar. Y es que la limpieza bucal infantil, junto a la adquisición del hábito de su mantenimiento, comportará que el adulto pueda conservar sus dientes para toda la vida. Por eso, es importante que esta práctica se inicie en el recién nacido, sin esperar a que aparezcan las primeras piezas dentarias, mediante una gasa de algodón humedecida en agua potable.

Esto se realiza por varias razones; una de ellas, obviamente, es para mantener la boca del bebé limpia de restos, y otra, es la de ir acostumbrándole a este hábito. En este sentido, generalmente por desconocimiento, muchos padres no inician la higiene bucal de sus hijos hasta cerca de los dos años (edad en la que ya se pueden empezar a usar los cepillos dentales). Y muchas veces puede que a esa edad hayan aparecido las primeras caries.

Para que esta rutina se convierta en imprescindible en el día a día de cualquier bebé o niño, conviene realizarla de la forma más amena posible:

• Llevar a cabo la higiene en un momento en el que el niño esté relajado y de buen humor, y no esperar al momento previo de ir a la cama que es cuando está más cansado o dormido.
• Negociar y dar opciones. Se puede preseleccionar los cepillos que consideremos adecuados para el niño y dejarle a él escoger cuál o cuáles quiere usar. Si el cepillo tiene su color o su personaje favorito, le entusiasmará más cepillarse los dientes.
• Proponer una actividad agradable para el niño, no a modo de chantaje ni recompensa, sino como un incentivo para hacer después del cepillado.
• Evitar amenazas, castigos y argumentos negativos. Siempre es más recomendable mostrar el lado positivo del cepillado: Nos cepillamos para cuidarnos, igual como hacemos con el cabello...
• Reservar un juguete para la hora del cepillado. Se puede usar una marioneta, un muñeco o algún objeto interesante con el que el niño sólo pueda jugar durante cepillado los dientes.

¿Qué son las caries?

Son perforaciones en los dientes. Son un trastorno muy común que suele aparecer en los niños y en los adultos jóvenes principalmente pero que puede afectar a cualquier persona con una higiene bucodental deficiente. Es la causa más frecuente de pérdida de los dientes en las personas jóvenes.

Las bacterias que normalmente se encuentran en la boca convierten los alimentos en ácidos, y estos ácidos junto con la saliva y restos de comida se mezclan formando una sustancia llamada placa, que se pega a los dientes. Si esta placa no se elimina de los dientes, se convierte en sarro, que puede ocasionar gingivitis y/o periodontitis.

La placa además daña el esmalte que recubre los dientes y crea pequeños orificios en los dientes que es a lo que llamamos caries. Las caries no suelen doler a menos que estén muy avanzadas y afecten a los nervios o que causen la fractura del diente.

La caries en los niños ocasiona una serie de secuelas a corto plazo, como maloclusiones, y a largo plazo, como infecciones, problemas estéticos, dificultades para la alimentación, además de las repercusiones médicas, emocionales y financieras. Según un informe de la OMS del año 2004, la caries dental afecta entre el 60% y el 90 % de la población escolar.

Los niños con caries precoz en la infancia tienen mayor riesgo de presentar nuevas caries en la dentición permanente, por ello es muy importante establecer los hábitos de una buena higiene bucal, y así asentar una base de descenso de caries interproximales en los adolescentes.

Además, la mayoría de las enfermedades orales como las caries tienen una relación directa con la ingesta de azúcares, una higiene deficiente, alcohol y tabaco o estrés. Por tanto, es necesario evitar en la medida de lo posible dichos hábitos.

LIMPIEZA BUCAL

Una correcta higiene bucal es el factor clave para prevenir la caries en la infancia y cualquier otra enfermedad oral. Y es responsabilidad de los padres al menos hasta que el niño tenga la habilidad motora adecuada para efectuar estos procedimientos, nunca antes de los 5 años. Es a partir de los 8 a 10 años de edad que el niño se considera autónomo para realizarlo por sí solo. Desde este momento y hasta la adolescencia se recomienda la supervisión de su higiene oral nocturna.

Es importante entender lo perjudicial que puede llegar a ser que los niños duerman sin eliminar los residuos alimenticios, ya que durante las horas de sueño se desarrolla y crece la microbiota bacteriana, hasta el punto de llegar a producir caries.

Las principales pautas a seguir son:

• Cepillarse los dientes. Después de que salgan los primeros dientes, se debe comenzar con la limpieza bucodental dos veces al día. El cepillo debe ser adecuado a la edad del niño y tener un diseño específico con un mango recto y largo, una empuñadura gruesa, cerdas suaves con las puntas redondeadas y un cabezal de tamaño compatible con la boca del niño. Se recomienda limpiar las superficies dentales laterales (linguales y vestibulares) con movimientos circulares y las superficies masticatorias con movimientos anteroposteriores.
• Usar pasta dental y flúor. Se debe complementar el cepillado con una pasta dental fluorada, aunque no se recomienda en niños que no hayan aprendido a escupir (generalmente, menores de dos años de edad). El flúor ha demostrado ser una herramienta segura y eficaz en la reducción de la caries y en la reversión de desmineralizaciones del esmalte dentario, pero hay que supervisar su administración en los niños, pues los posibles efectos secundarios, como la irritación de los tejidos blandos, etc.
• Utilizar hilo dental. El hilo dental es indispensable en una buena limpieza bucal para remover la placa bacteriana acumulada en los espacios interdentales, lo que evita el riesgo de la caries entre los dientes.

VÍDEO: https://www.youtube.com/watch?v=xIeygf1cWmM

BIBLIOGRAFÍA DE INTERÉS:

1. DENTAID S.L. Higiene bucal infantil. Cuidado específico para bebés y niños[Internet]. España: Dentaid; Fecha de publicación: 02/05/2009 [revisado: 02/05/2009; consultado: 25/11/2017]. Disponible en: http://www.dentaid.es/es/higiene-bucal-infantil
2. Blanca Longás Bravo. Estudio sobre las caries en una población infantil en la comunidad de Madrid Año 2009. Tesis Doctoral. Universidad de Sevilla. Facultad de Odontología. Sevilla; 2009. Disponible en: http://fondosdigitales.us.es/tesis/tesis/1665/estudio-sobre-la-caries-en-una-poblacion-infantil-en-la-comunidad-de-madrid-ano-2009/#description
3. MedlinePlus. Caries dentales. [Internet]. EE.UU: MedlinePlus: Fecha de publicación: 02/22/2016 [revisado: 02/22/2016; consultado: 25/11/2017]. Disponible en: https://medlineplus.gov/spanish/ency/article/001055.htm 

REFLEXIÓN FINAL

Bueno chicos, ha llegado el final de este curso aunque nos queden los exámenes todavía. Espero que salgan bien, sé que hemos dado todo lo que hemos podido así que nada tiene porqué salir mal.
Ahora que ya he pasado este curso, con mejores o peores notas, lo que puedo decir, es que, aunque no hemos tenido prácticas por ahora, estoy ansiosa por tenerlas, y lo más importante, es que, yo no elegí enfermería desde el principio pero si tuviese que escoger ahora mi carrera, VOLVERÍA A ESCOGER ENFERMERÍA.
Y con respecto a esta asignatura, pues se agradece mucho que haya algo de números entre tanta teoría, es algo difícil pero nada que no pueda sacarse con un poco de tiempo y dedicación, como todo.
¡¡Suerte a todos y espero que estéis igual de felices con vuestra elección como lo estoy yo!!!

¿CÓMO SABER SI UNA VARIABLE SIGUE UNA DISTRIBUCIÓN NORMAL?

Para realizar un test de hipótesis, es necesario que las variables sigan una distribución normal, por tanto, para determinar si una variable sigue una distribución normal, existen dos pruebas, la prueba de Shapiro-Wilks y la prueba de Kolmogorov-Smirnov.

PRUEBA DE KOLMOGOROV-SMIRNOV
Cuando la prueba Kolmogorov-Smirnov se aplica para contrastar la hipótesis de normalidad de la población, el estadístico de prueba es la máxima diferencia:

siendo Fn(x) la función de distribución muestral y Fo(x) la función teórica o correspondiente a la población normal especificada en la hipótesis nula.
La distribución de Kolmogorov-Smirnov es independiente de la distribución poblacional especificada en la hipótesis nula.

PRUEBA DE SHAPIRO-WILKS
Cuando la muestra es como máximo de tamaño 50 se puede contrastar la normalidad con la prueba de shapiro Shapiro-Wilks. La fórmula es la siguiente: 

donde D es la suma de las diferencias.
Se rechazará la hipótesis nula de normalidad si W es menor que el valor proporcionado por la tabla elaborada por los autores para el tamaño muestral y el nivel de significación dado.

TAU DE KENDALL

El último test de hipótesis que estudiaremos, se llama, Tau de Kendall y se utiliza para comparar variables cuantitativas.

Las fórmulas son las siguientes:

 T = |B1| / (Sy/Sx * √ (n - 1) )

Gracias a ellas, podremos representar los datos en un gráfico y después obtener el valor de tau, y, tras compararlo con el valor que nos proporciona la tabla, ver si es correcto o no rechazar la hipótesis nula.

SESIONES TEÓRICAS DE ESTDÍSTICA Y TIC’s: TEMA 10: HIPÓTESIS ESTADÍSTICAS. TEST DE HIPÓTESIS

Para controlar los errores aleatorios, podemos utilizar el cálculo de intervalos de confianza pero también podemos realizar los test de hipótesis. Estos consisten en plantear una hipótesis nula sobre un estudio y calcular el error que se cometería al rechazarla o al aceptarla.

TIPOS DE TEST DE HIPÓTESIS Y CUÁNDO UTILIZAR CADA UNO

DEPENDIENTE INDEPENDIENTE	Cualitativa 2 Grupos	Cualitativa > 2 Grupos	Cuantitativa
Cualitativa 2 Grupos	Chi cuadrado T comparación proporciones P. exacta de Fisher P. Mc Nemar	Chi cuadrado Q de Cochran	T student U. de Mann- Whitney T. Wilcoxon
Cualitativa > 2 Grupos	Chi cuadrado Q. de Cochran	Chi cuadrado Q. de Cochrann	A. varianza Kruskall-Wallis F. Friedman
Cuantitativa	Regresión logística	Regresión logística	Regresión lineal: Correl. Pearson Correl. Spearman

ERRORES DE HIPÓTESIS

El error que se comete al aceptar la hipótesis nula, es lo que se llama, error alfa.
Por el contrario, si el error que cometemos es, rechazar la hipótesis nula cuando es la verdadera, se llama error beta.
El error máximo que se acepta en los estudios de ciencias de la salud es de p<0.05, es decir, de un máximo de un 5%. A esto se le denomina significación estadística. Para calcular estos errores, utilizamos los test de hipótesis:

CHI CUADRADO DE PEARSON

Sirve para comparar dos variables cualitativas.
Suponemos que la Ho (hipótesis nula) es cierta, y calculamos el tamaño del error si la aceptásemos, con la siguiente fórmula:

La O, son los resultados observados y la E, son los resultados esperados, que se calculan multiplicando la suma de las filas por la suma de las columnas y dividiéndolo entre el total.

Una vez hemos obtenido un resultado de chi cuadrado, es hora de compararlo con el valor de la tabla, buscando, en la fila del grado de libertad de nuestor estudio y en la columna del erros 0.05.

Si el valor de chi cuadrado que nos ha salido a nosotros es menor que el valor que nos da la tabla, quiere decir que hay que aceptar la hipótesis nula. Por el contrario, si nuestro valor de chi cuadrado es mayor que el valor de la tabla, la rechazamos.

El grado de libertad de este test se calcula: (columnas – 1) * (filas – 1)

TABLA CHI CUADRADO

T DE STUDENT

Este test de hipótesis sirve para comparar variables cualitativas dicotómicas con cuantitativas. Para realizar el test, son necesarias las siguientes, fórmulas:

Tras obtener un valor de t, igual que en el test anterior, compararemos nuestro resultado con el valor que aparezca en la tabla y, si nuestro valor de t es menor que el de la tabla, aceptamos la hipótesis nula y si es mayor, la rechazamos.

El grado de libertad de este test se calcula: n1 + n2 - 2

TABLA T STUDENT

TEST DE ANOVA

Es un análisis de la varianza, que prueba la hipótesis de que las medias de dos o más poblaciones son iguales.
No entro en detalles puesto que solamente se nos pide que conozcamos para qué se utiliza.

SEMINARIO 5: EXPOSICIÓN DE LOS TRABAJOS DE INVESTIGACIÓN

En este seminario, cada grupo expuso sus trabajos de investigación. Los grupos fueron los mismos que en el seminario 2.

• El primer grupo, expuso su trabajo sobre El Sobrepeso en los Niños Escolarizados en Edad Infantil.
• El segundo, es decir, el de mi grupo, sobre El Consumo de Narguile en la Sociedad 
• Y el tercero sobre La Prevalencia de los Mitos del Amor Romántico en la Juventud.

Tras cada exposición el profesor apuntaba algunos detalles que le habían parecido interesantes y nos daba algunos consejos que nos serían útiles en futuras exposiciones.

SESIONES TEÓRICAS DE ESTDÍSTICA Y TIC’s: TEMA 9: ESTADÍSTICA INFERENCIAL

Se trata de obtener información sobre una población, y a partir de los datos obtenidos, deducir la información sobre el resto de la población.

La población que se estudia se llama población de estudio y el grupo de personas sobre las que se realiza el estudio, se llama muestra. El tamaño de dicho grupo se denomina tamaño muestral. El conjunto de procedimientos estadísticos se llama inferencia estadística y los procedimientos para elegir la muestra se llaman técnicas de muestreo.

Si la muestra se elige al azar, se cometerá un error probabilístico o aleatorio. 

La medida que queremos obtener de la población se llama parámetro y la medida de la variable de estudio obtenida en la muestra se llama estimador.

ERROR ESTÁNDAR

• Es la medida que trata de captar la variabilidad de los valores del estimador
• Cuánto más pequeño es el error estándar de un estimador, más nos podemos fiar del valor de la muestra.
• Se calcula de la siguiente manera:
• Para una media: e = s/√n 
• Para una proporción: e = √(p(1 - p) / n)

TEOREMA CENTRAL DEL LÍMITE 

• Para estimadores que siguen una distribución normal con media de la población y desviación típica igual al error estándar del estimador que se trate.

INTERVALOS DE CONFIANZA

• Son un medio de conocer el parámetro en una población midiendo el error que tiene que ver con el azar

PROCEDIMIENTO MUESTRAL

• La muestra debe ser representativa del resto de la población
• Se debe elegir al azar la población de la que se extraiga la muestra

TIPOS DE MUESTREO

• Probabilístico: todos los sujetos de la población tienen una probabilidad distinta de cero de ser elegidos para la muestra
• Aleatorio simple
• De sorteo o rifa
• Tabla de números aleatorios
• Aleatorio sistemático
• Estratificado
• Conglomerado
• No probabilístico: puede haber personas que no tengan probabilidades de estar en la muestra o que se desconozca su probabilidad

TAMAÑO DE LA MUESTRA 

• n = z² * S² / e² 
• Si tras este cálculo, se cumple el resultado n > n(n-1), el cálculo acaba aquí 
• Si no se cumple ese resultado, se realiza lo siguiente: 
• n' = n/1 + (n/N)

SESIONES TEÓRICAS DE ESTDÍSTICA Y TIC’s: TEMA 8: MEDIDAS DE TENDENCIA CENTRAL, POSICIÓN Y DISPERSIÓN

1. MEDIDAS DE TENDENCIA CENTRAL

• Media: es el valor central de los datos. Es la suma de todos los datos dividida entre el número de datos.
• Moda: es el valor que más se repite, el que aparece con mayor frecuencia.
• Mediana: es el valor de una observación tal que deja a un 50% de los datos menor y otro 50% mayor.
• Propiedad: robustez.

2. MEDIDAS DE POSICIÓN O CUANTILES

• Percentiles: dividen la muestra ordenada en 100 partes. 
• Deciles: dividen la muestra ordenada en 10 partes.
• Cuartiles: dividen la muestra ordenada en 4 partes.

3. MEDIDAS DE DISPERSIÓN

• Rango o recorrido: diferencia entre el mayor y el menor valor de la muestra.
• Desviación media: media aritmética de las distancias de cada observación con respecto a la media de la muestra.
• Desviación típica o estándar: sirve para calcular el error que se comete si representamos una variable por su media.
• Varianza: expresa lo mismo que la desviación estándar pero al cuadrado.
• Recorrido intercuartílico: es la diferencia entre el tercer y el primer cuartil.
• Coeficiente de variación: compara la heterogeneidad de dos series numéricas.

4. DISTRIBUCIÓN NORMAL

Es una de las distribuciones de probabilidad de variable continua más frecuentes. Se representa mediante la campana de Gauss. 

5. ASIMETRÍA Y CURTOSIS

Coeficiente de asimetría de una variable: grado de simetría de la distrubición de los datos en torno a su media.
Asimetrías: 

• G1 = 0: distribución simétrica 
• G1 > 0: distribución asimétrica positiva
• G1 < 0: distribución asimétrica positiva

Curtosis o apuntamiento de la curva: mide el grado de concentración de los valores que la variable toma en torno a su media.

6. TIPIFICACIÓN DE VARIABLES. DISTRIBUCIÓN NORMAL ESTÁNDAR

La distribución normal estándar, o tipificada o reducida, es aquella que tiene por media el valor cero, μ =0, y por desviación típica la unidad, σ =1.
Para poder utilizar la tabla tenemos que transformar la variable X que sigue una distribución N(μ, σ) en otra variable Z que siga una distribución N(0, 1).

TABLA DISTRIBUCIÓN NORMAL

SEMINARIO 4: MEDIDAS DE TENDENCIA CENTRAL, POSICIÓN Y DISPERSIÓN. ESTADÍSTICA INFERENCIAL: MUESTREO Y ESTIMACIÓN. HIPÓTESIS ESTADÍSTICAS. TEST DE HIPÓTESIS.

En el seminario 4, el profesor nos adelantó el contenido de las sesiones teóricas, correspondientes a los temas 8, 9 y 10 e hicimos algunos ejercicios de repaso de temas anteriores y nuevos, como por ejemplo, los test de hipótesis. Explicó el procedimiento del test de Chi cuadrado de Pearson.

SESIONES TEÓRICAS DE ESTDÍSTICA Y TIC’s: TEMA 7: INTRODUCCIÓN A LA BIOESTADÍSTICA

1. ESTADÍSTICA

Ciencia que utiliza conjuntos de datos numéricos para obtener, a partir de ellos, inferencias basadas en el cálculo de probabilidades., es decir, es el conjunto de conocimientos que sirven para aprender en base a estudios realizados previamente.
Existen diferentes tipos de métodos de medición para los diferentes tipos de variables.

2. ESCALAS DE MEDIDA

• ESCALA NOMINAL: Sirve para comprobar si dos variables son iguales o diferentes. 
• ESCALA ORDINARIA: Sirve para comprobar si dos variables son iguales o diferentes, y en el caso de ser diferentes, averiguar cuál de las dos es mayor. 
• ESCALA DE INTERVALO: Tiene las características de las dos escalas anteriores y además expresa el intervalo en el que se encuentra la variable. 
• ESCALA DE RAZÓN: Es el nivel más alto de medición. Es la que permite obtener más información de las tres. Además de las características de las escalas anteriores, posee el cero absoluto, es decir, la ausencia de lo que se estudia. 3. TIPOS DE VARIABLES

3. TIPOS DE VARIABLES

• CUALITATIVAS: Se refieren a propiedades que no pueden ser medidas. 
• Nominales: se miden con escalas nominales 
• Dicotómicas: hay dos niveles, por ejemplo, puede responderse con un si o un no. 
• Policotómicas: tiene más de dos niveles, por ejemplo, el estado civil: soltero, casado, viudo, divorciado… 
• Ordinales: establecen un orden o jerarquía, por ejemplo: muy bien, bien, regular, mal o muy mal. 
• CUANTITATIVAS: Hacen referencia a variables que pueden medirse. 
• Discreta: toma valores de números enteros. 1, 2, 3… 
• Continua: puede tomar valores numéricos dentro de un intervalo, es decir, 1,2, 1,4, 5,6… (números decimales) 

4. VARIABLES: REPRESENTACIÓN DE DATOS

• Tablas de frecuencia: son tablas que representan los datos de frecuencia y las categorías de las variables en filas y columnas. 
• Frecuencia relativa: es la frecuencia absoluta entre el número total de la muestra. Toma valores entre 0 y 1. 5. VARIABLES CONTINUAS: REPRESENTACIÓN DE DATOS

5. VARIABLES CONTINUAS: REPRESENTACIÓN DE DATOS

• Definir los intervalos y sus extremos 
• Definir la amplitud o la distancia entre los extremos de los intervalos 
• Calcular la marca de clase de cada intervalo 
• Calcular el recorrido: diferencia entre el valor más alto y el más bajo 
• Calcular el intervalo: raíz cuadrada del número de datos observado. 
• Calcular la amplitud: dividir el recorrido entre el número de intervalos 6. 

6. REPRESENTACIONES GRÁFICAS

Son imágenes de las ideas, transmiten al receptor los datos de manera rápida y fácil, pero no reemplazan al texto.
Deben ser visualmente claros, representar gráficamente las conclusiones del estudio y no ser confusos ni estar sobrecargado de datos.

• REACCIONES LOCALES MÁS FRECUENTES 
• Diagrama de barras (pictogramas): para variables cualitativas, nominales y policotómicas. 

• HISTOGRAMAS Y POLÍGONOS DE FRECUENCIA 
• Histograma: sirve para representar variables continuas. 
• Las marcas de clase: es el punto medio de cada intervalo 
• El polígono de frecuencia: es el polígono que se forma al unir las marcas de clase 

7. GRÁFICOS 

• GRÁFICO DE TRONCO Y HOJAS: Sirve para expresar variables cuantitativas y continuas

• GRÁFICO DE SECTORES: Se utiliza para variables dicotómicas y cualitativas

• GRÁFICO PARA DATOS BIDIMENSIONALES: sirve para representar variables cuantitativas 
• GRÁFICO PARA DATOS MULTIDIMENSIONALES: diagrama de estrellas

SESIONES TEÓRICAS DE ESTADÍSTICA Y TIC’s: TEMA 6: LA ETAPA EMPÍRICA DE LA INVESTIGACIÓN. EL DISEÑO, MATERIAL Y MÉTODOS.

1. MATERIAL Y MÉTODOS

• Es necesario seguir los siguientes pasos: 
• Planificar la recogida de datos 
• Registrar y procesar los datos 
• Ejecutar la recogida de datos 
• Analizar los datos 

2. ASIGNACIÓN DEL DISEÑO EN FUNCIÓN DE LA PREGUNTA DE INVESTIGACIÓN

• Analíticos 
• Experimentales 
• Casi experimentales 

3. MEDIDAS DE FRECUENCIA EN ESTUDIOS DESCRIPTIVOS

• Debemos tener claro que es lo que queremos medir, la medida de prevalencia. 
• Saber qué es lo que está pasando en una medida de tiempo, la incidencia. 
• Describir la frecuencia de aparición de nuevos casos 
• Incidencia acumulada: calcula la proporción de incidencia, es decir, el riesgo de que se produzca un fenómeno. 

• PREVALENCIA = Nº DE INDIVIDUOS CON LA ENFERMEDAD EN UN TIEMPO ESPECÍFICO / Nº DE INDIVIDUOS EN LA POBLACIÓN EN UN PUNTO EN EL TIEMPO 

La prevalencia no puede ser menor que cero ni mayor que uno. Es adimensional y adopta valores entre cero y uno.

• INCIDENCIA = Nº DE NUEVOS CASOS DETECTADOS DURANTE EL SEGUIMIENTO QUE DESARROLLAN LA ENFERMEDAD / Nº DE SUJETOS LIBRES DE ENFERMEDAD AL COMIENZO DEL SEGUIMIENTO 

• INCIDENCIA ACUMULADA = Nº TOTAL DE CASOS NUEVOS EN UN TIEMPO DETERMINADO / POBLACIÓN A RIESGO EN EL MOMENTO INICIAL

4. TASA DE INCIDENCIA O DENSIDAD DE INCIDENCIA

• Hace referencia a la velocidad con la que aparecen nuevos casos.
• Se calcula de la siguiente manera:

• TASA DE INCIDENCIA = Nº DE CASOS NUEVOS / PERSONAS - TIEMPO A RIESGO 

5. ESTUDIOS DE RIESGO Y EXPERIMENTALES

• MEDIDAS DE ASOCIACIÓN 
• INCIDENCIA EN NO EXPUESTOS = Nº DE CASOS NUEVOS ENTRE LOS NO EXPUESTOS / Nº TOTAL DE INDIVIDUOS NO EXPUESTOS 
• INCIDENCIA EN EXPUESTOS = Nº DE CASOS NUEVOS ENTRE EXPUESTOS / Nº TOTAL DE INDIVIDUOS EXPUESTOS 

• RIESGO RELATIVO 

Es la razón entre el riesgo de los expuestos y el de los no expuestos. Si el valor del riesgo relativo es 1, quiere decir que la incidencia en expuestos y no expuestos es la misma, por lo que aceptamos la hipótesis nula.

6. ESTUDIOS DE CASOS Y CONTROLES. ESTIMACIÓN DE LA MAGNITUD DE ASOCIACIÓN.

En este tipo de estudios se realiza una comparación entre un grupo que presenta la variable independiente y otro que no.
Es necesario calcular la ODDS RATIO, que se calcula dividiendo la ODDS casos entre la ODDS controles.

• Si es igual a 1, se acepta la hipótesis nula 
• Si es mayor que 1, los casos tienen mayor riesgo de exposición al factor 
• Si es menor que 1 los controles tienen mayor riesgo de exposición al factor